Recent Advances in Deep Learning for Routing Problems
25 Mar 2022 | graphs deep-learning combinatorial-optimization travelling-salesperson-problemTL;DR Developing neural network-driven solvers for combinatorial optimization problems such as the Travelling Salesperson Problem have seen a surge of academic interest recently. This blogpost presents a Neural Combinatorial Optimization pipeline that unifies several recently proposed model architectures and learning paradigms into one single framework. Through the lens of the pipeline, we analyze recent advances in deep learning for routing problems and provide new directions to stimulate future research towards practical impact.
- Background on Combinatorial Optimization Problems
- Unified Neural Combinatorial Optimization Pipeline
- Characterizing Prominent Papers via the Pipeline
- Recent Advances and Avenues for Future Work
- Summary
Background on Combinatorial Optimization Problems
Combinatorial Optimization is a practical field in the intersection of mathematics and computer science that aims to solve constrained optimization problems which are NP-Hard. NP-Hard problems are challenging as exhaustively searching for their solutions is beyond the limits of modern computers. It is impossible to solve NP-Hard problems optimally at large scales.
Why should we care? Because robust and reliable approximation algorithms to popular problems have immense practical applications and are the backbone of modern industries. For example, the Travelling Salesperson Problem (TSP) is the most popular Combinatorial Optimization Problems (COPs) and comes up in applications as diverse as logistics and scheduling to genomics and systems biology.
The Travelling Salesperson Problem is so famous, or notorious, that it even has an xkcd comic dedicated to it!
TSP and Routing Problems
TSP is also a classic example of a Routing Problem – Routing Problems are a class of COPs that require a sequence of nodes (e.g., cities) or edges (e.g., roads between cities) to be traversed in a specific order while fulfilling a set of constraints or optimising a set of variables. TSP requires a set of edges to be traversed in an order that ensures all nodes are visited exactly once. In the algorithmic sense, the optimal “tour” for our salesperson is a sequence of selected edges that provides the minimal distance or time taken over a Hamiltonian cycle, see Figure 1 for an illustration.
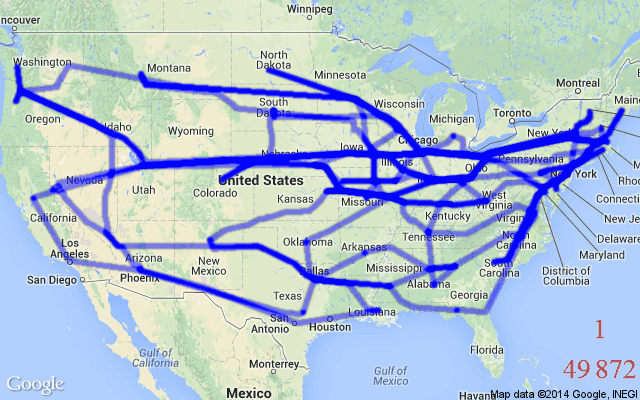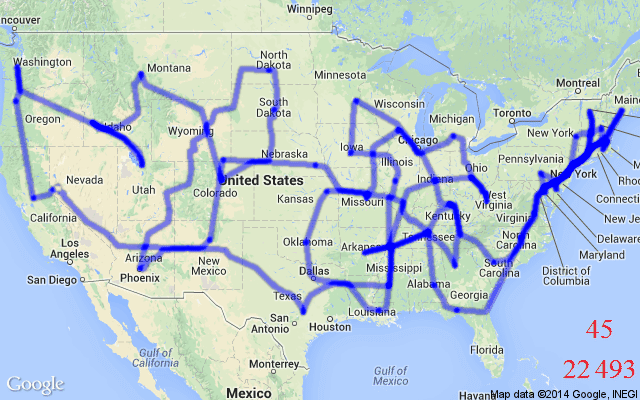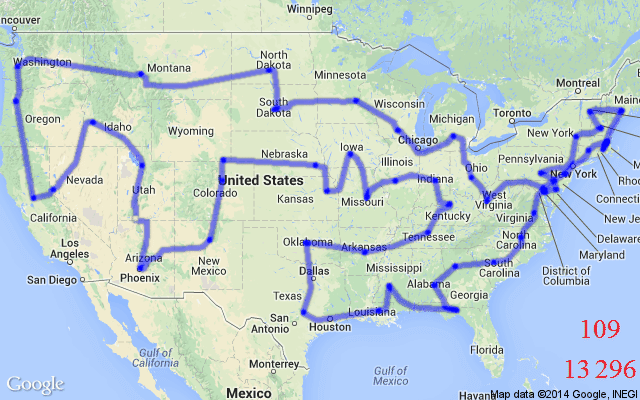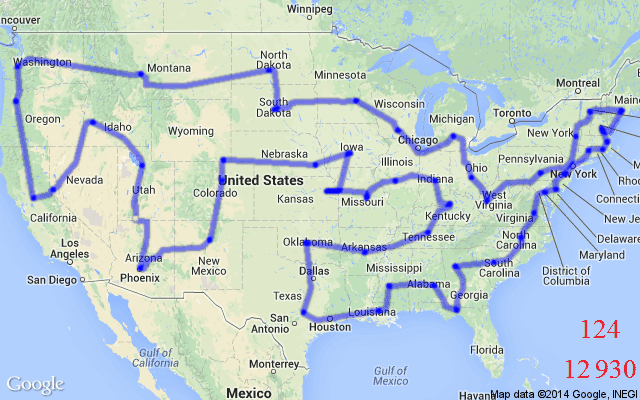
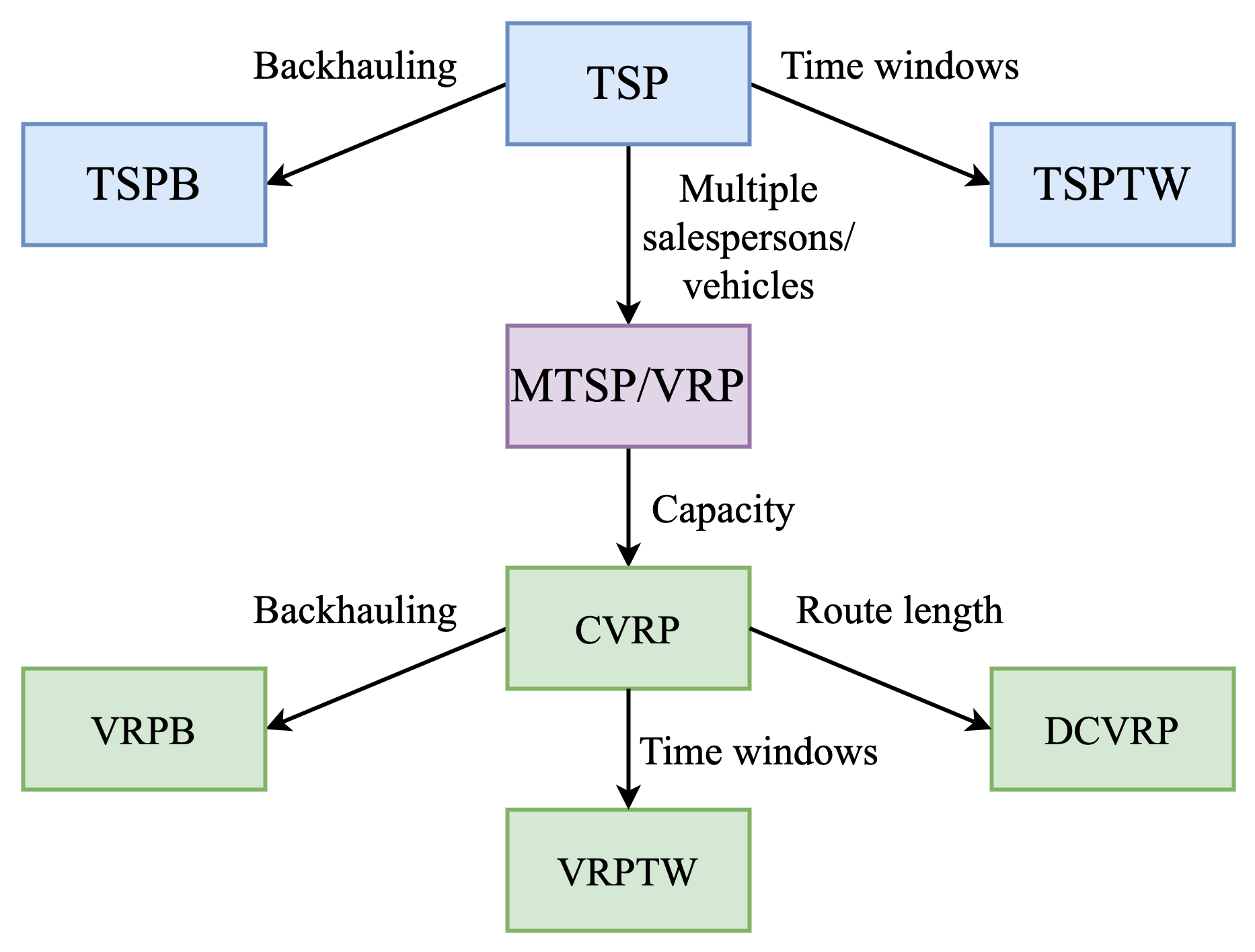
In real-world and practical scenarios, Routing Problems, or Vehicle Routing Problems (VRPs), can involve challenging constraints beyond the somewhat vanilla TSP; they are generalisations of TSP. For example, the TSP with Time Windows (TSPTW) adds a “time window” contraint to nodes in a TSP graph. This means certain nodes can either be active or inactive at a given time, i.e., they can only be visited during certain intervals. Another variant, the Capacitated Vehicle Routing Problem (CVRP) aims to find the optimal routes for a fleet of vehicles (i.e., multiple salespersons) visiting a set of customers (i.e., cities), with each vehicle having a maximum carrying capacity.
Deep Learning to solve Routing Problems
Developing reliable algorithms and solvers for routing problems such as VRPs requires significant expert intuition and years of trial-and-error. For example, the state-of-the-art TSP solver, Concorde, leverages over 50 years of research on linear programming, cutting plane algorithms and branch-and-bound; here is an inspiring video on its history. Concorde can find optimal solutions up to tens of thousands of nodes, but with extremely long execution time. As you can imagine, designing algorithms for complex VRPs is even more challegning and time consuming, especially with real-world constraints such as capacities or time windows in the mix.
This has led the machine learning community to ask the following question:
Can we use deep learning to automate and augment expert intuition required for solving COPs?
See this masterful survey from Mila for more in-depth motivation: [Bengio et al., 2020].
Neural Combinatorial Optimization
Neural Combinatorial Optimization is an attempt to use deep learning as a hammer to hit the COP nails. Neural networks are trained to produce approximate solutions to COPs by directly learning from problem instances themselves. This line of research started at Google Brain with the seminal Seq2seq Pointer Networks and Neural Combinatorial Optimization with RL papers. Today, Graph Neural Networks are usually the architecture of choice at the core of deep learning-driven solvers as they tackle the graph structure of these problems.
Neural Combinatorial Optimization aims to improve over traditional COP solvers in the following ways:
-
No handcrafted heuristics. Instead of application experts manually designing heuristics and rules, neural networks learn them via imitating an optimal solver or via reinforcement learning (we describe a pipeline for this in the next section).
-
Fast inference on GPUs. Traditional solvers can often have prohibitive execution time for large-scale problems, e.g., Concorde took 7.5 months to solve the largest TSP with 109,399 nodes. On the other hand, once a neural network has been trained to approximately solve a COP, they have significantly favorable time complexity and can be parallelized via GPUs. This makes them highly desirable for real-time decision-making problems, especially routing problems.
-
Tackling novel and under-studied COPs. The development of problem-specific COP solvers for novel or understudied problems that have esoteric constraints can be significantly sped up via neural combinatorial optimization. Such problems often arise in scientific discovery or computer architecture, e.g., an exciting success story is Google’s chip design system that will power the next generation of TPUs. You read that right – the next TPU chip for running neural networks has been designed by a neural network!
Unified Neural Combinatorial Optimization Pipeline
Using TSP as a canonical example, we now present a generic neural combinatorial optimization pipeline that can be used to characterize modern deep learning-driven approaches to several routing problems.
State-of-the-art approaches for TSP take the raw coordinates of cities as input and leverage GNNs or Transformers combined with classical graph search algorithms to constructively build approximate solutions. Architectures can be broadly classified as: (1) autoregressive approaches, which build solutions in a step-by-step fashion; and (2) non-autoregressive models, which produce the solution in one shot. Models can be trained to imitate optimal solvers via supervised learning or by minimizing the length of TSP tours via reinforcement learning.

The 5-stage pipeline from Joshi et al., 2021 brings together prominent model architectures and learning paradigms into one unified framework. This will enable us to dissect and analyze recent developments in deep learning for routing problems, and provide new directions to stimulate future research.
(1) Defining the problem via graphs
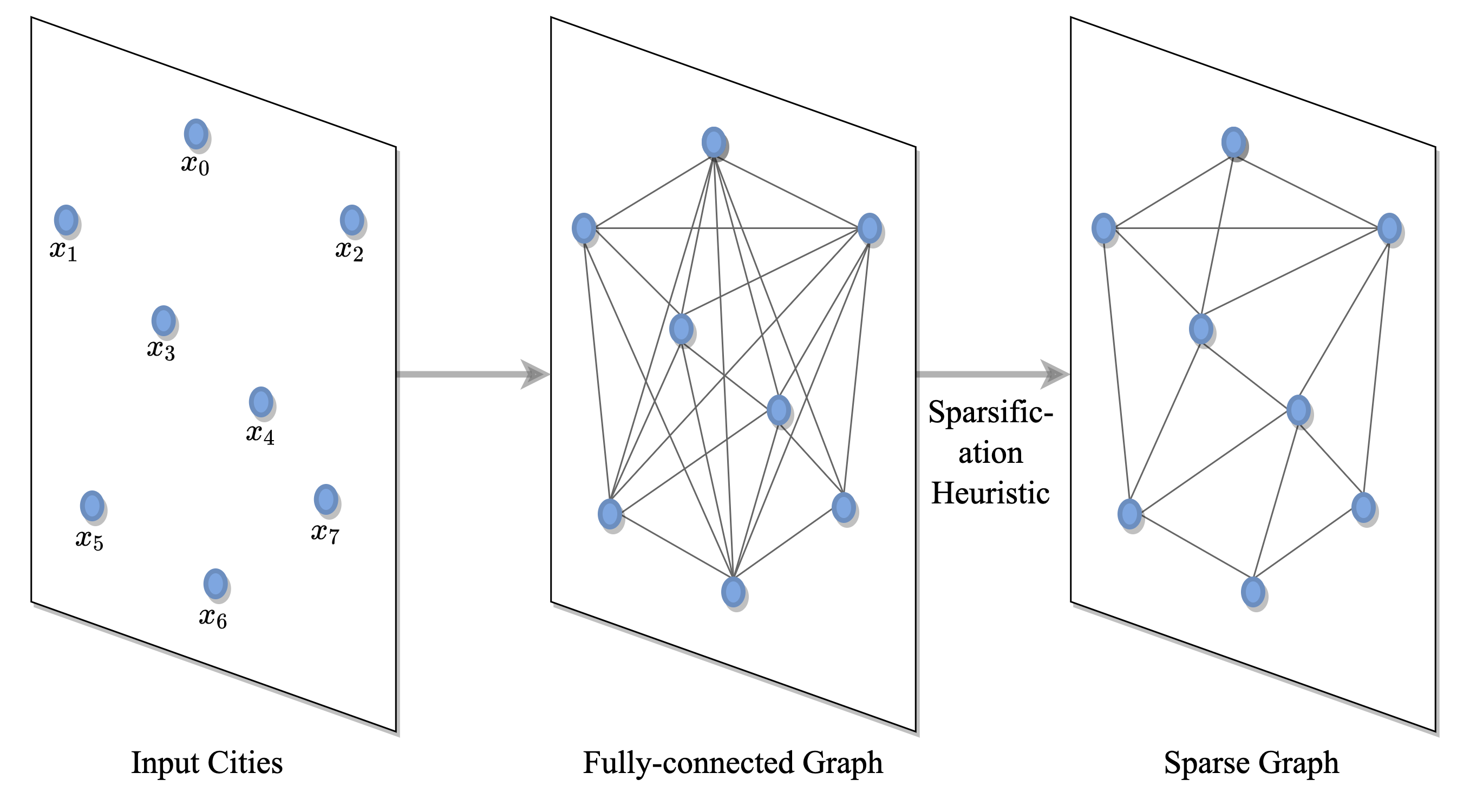
TSP is formulated via a fully-connected graph where nodes correspond to cities and edges denote roads between them. The graph can be sparsified via heuristics such as k-nearest neighbors. This enables models to scale up to large instances where pairwise computation for all nodes is intractable [Khalil et al., 2017] or learn faster by reducing the search space [Joshi et al., 2019].
(2) Obtaining latent embeddings for graph nodes and edges
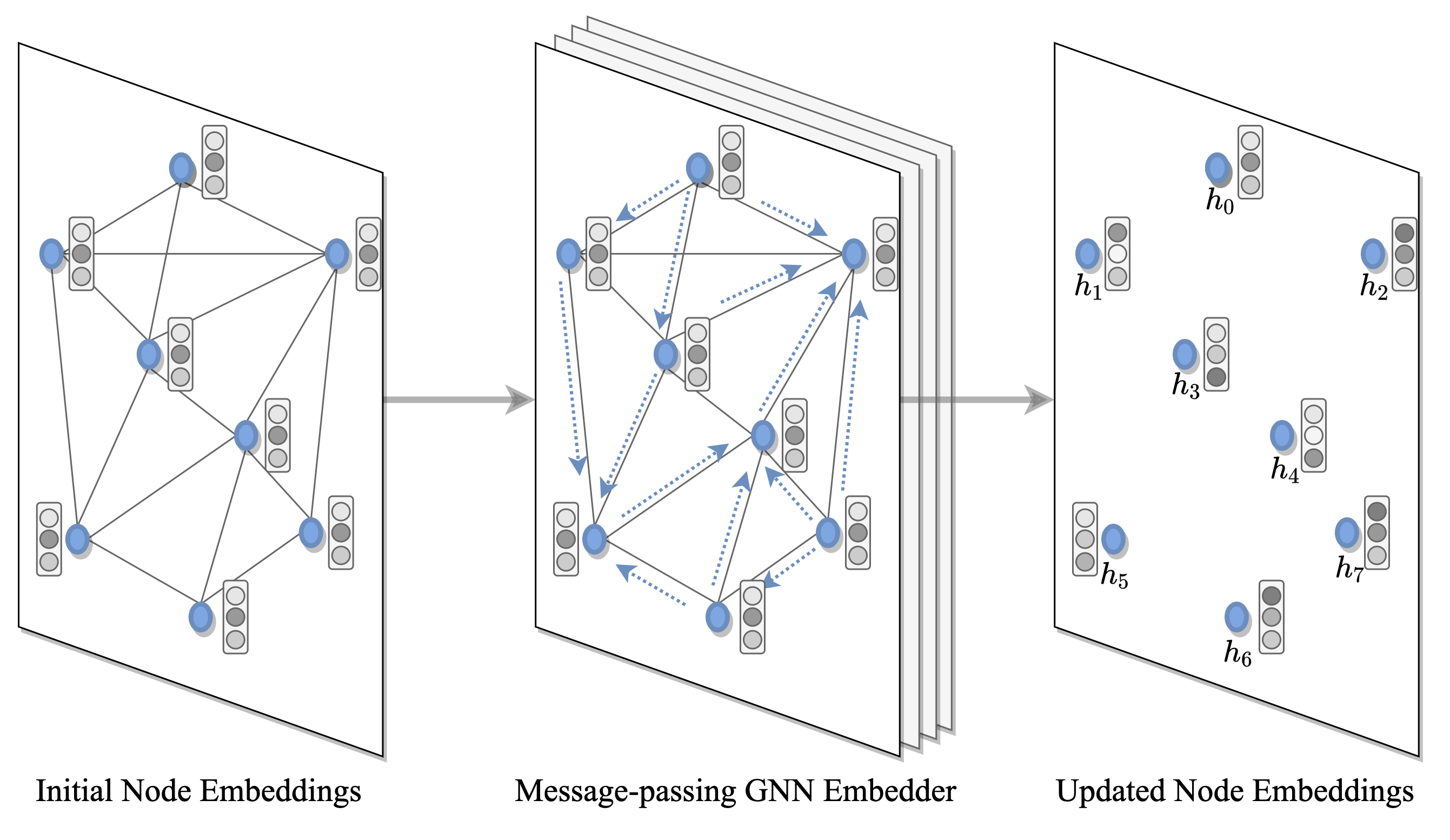
A GNN or Transformer encoder computes hiddden representations or embeddings for each node and/or edge in the input TSP graph. At each layer, nodes gather features from their neighbors to represent local graph structure via recursive message passing. Stacking $L$ layers allows the network to build representations from the $L$-hop neighborhood of each node.
Anisotropic and attention-based GNNs such as Transformers [Deudon et al., 2018, Kool et al., 2019] and Gated Graph ConvNets [Joshi et al., 2019] have emerged as the default choice for encoding routing problems. The attention mechanism during neighborhood aggregation is critical as it allows each node to weigh its neighbors based on their relative importance for solving the task at hand.
Importantly, the Transformer encoder can be seen as an attentional GNN, i.e., Graph Attention Network (GAT), on a fully-connected graph. See this blogpost for an intuitive explanation.
(3 + 4) Converting embeddings into discrete solutions
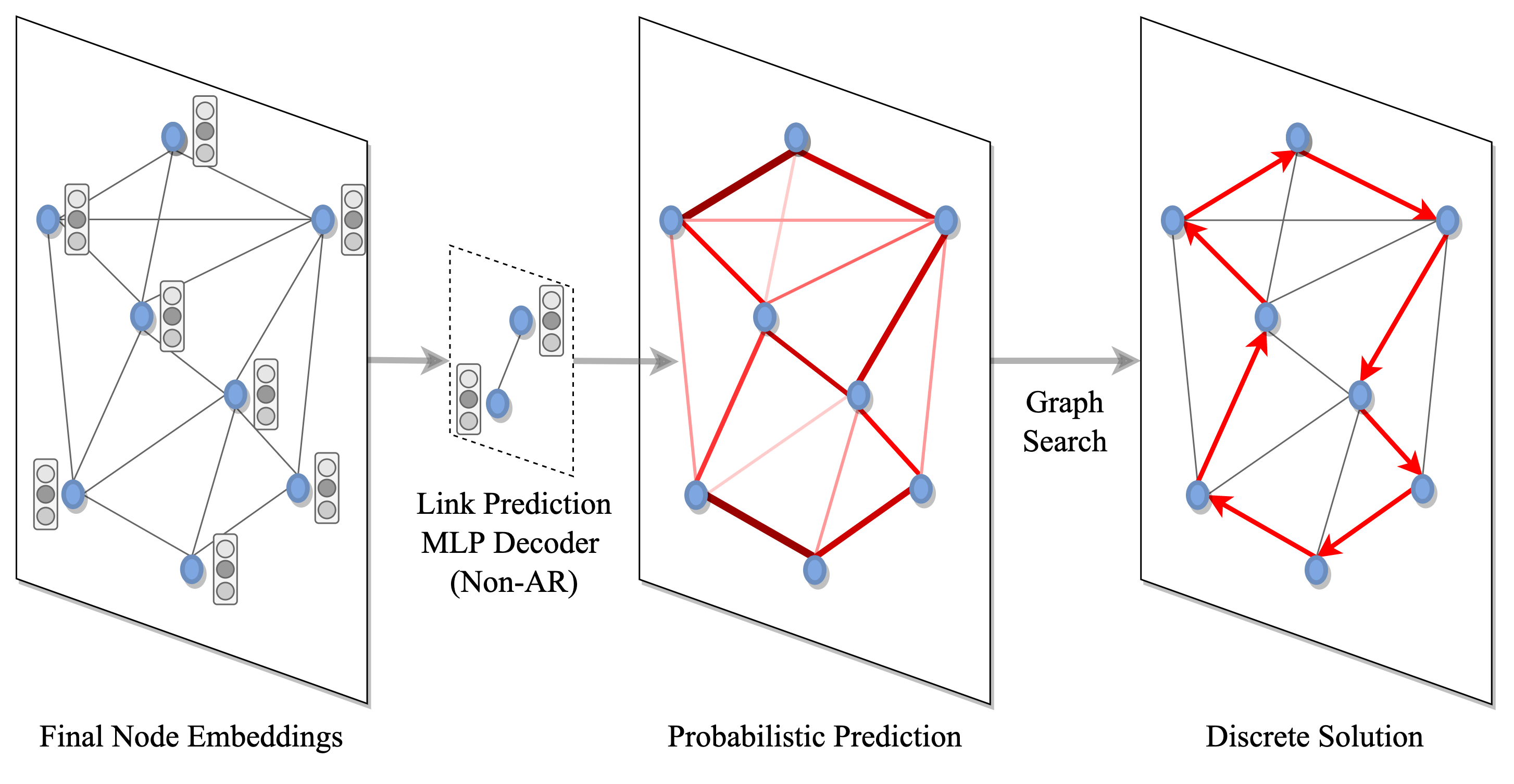
Once the nodes and edges of the graph have been encoded into latent representations, we must decode them into discrete TSP solutions. This is done via a two-step process: Firstly, probabilities are assigned to each node or edge for belonging to the solution set, either independent of one-another (i.e., Non-autoregressive decoding) or conditionally through graph traversal (i.e., Autoregressive decoding). Next, the predicted probabilities are converted into discrete decisions through classical graph search techniques such as greedy search or beam search guided by the probabilistic predictions (more on graph search later, when we discuss recent trends and future directions).
The choice of decoder comes with tradeoffs between data-efficiency and efficiency of implementation: Autoregressive decoders [Kool et al., 2019] cast TSP as a Seq2Seq or language translation task from a set of unordered cities to an ordered tour. They explicitly model the sequential inductive bias of routing problems through step-by-step selection of one node at a time. On the other hand, Non-autoregressive decoders [Joshi et al., 2019] cast TSP as the task of producing edge probability heatmaps. The NAR approach is significantly faster and better suited for real-time inference as it produces predictions in one shot instead of step-by-step. However, it ignores the sequential nature of TSP, and may be less efficient to train when compared fairly to AR decoding [Joshi et al., 2021].
(5) Training the model
Finally, the entire encoder-decoder model is trained in an end-to-end fashion, exactly like deep learning models for computer vision or natural language processing. In the simplest case, models can be trained to produce close-to-optimal solutions via imitating an optimal solver, i.e., via supervised learning. For TSP, the Concrode solver is used to generate labelled training datasets of optimal tours for millions of random instances. Models with AR decoders are trained via teacher-forcing to output the optimal sequence of tour nodes [Vinyals et al., 2015], while those with NAR decoders are trained to identify edges traversed during the tour from non-traversed edges [Joshi et al., 2019].
However, creating labelled datasets for supervised learning is an expensive and time-consuming process. Especially for very large problem instances, the exactness guarentees of optimal solvers may no longer materialise, leading to inexact solutions being used for supervised training. This is far from ideal from both practical and theoretical standpoints [Yehuda et al., 2020].
Reinforcement learning is a elegant alternative in the absence of groundtruth solutions, as is often the case for understudied problems. As routing problems generally require sequential decision making to minimize a problem-specific cost functions (e.g., the tour length for TSP), they can elegantly be cast in the RL framework which trains an agent to maximize a reward (the negative of the cost function). Models with AR decoders can be trained via standard policy gradient algorithms [Kool et al., 2019] or Q-Learning [Khalil et al., 2017].
Characterizing Prominent Papers via the Pipeline
We can characterize prominent works in deep learning for TSP through the 5-stage pipeline. Recall that the pipeline consists of: (1) Problem Definition → (2) Graph Embedding → (3) Solution Decoding → (4) Solution Search → (5) Policy Learning. Starting from the Pointer Networks paper by Oriol Vinyals and collaborators, the following table highlights in Red the major innovations and contributions for several notable and early papers.
| Paper | Definition | Graph Embedding | Solution Decoding | Solution Search | Policy Learning |
|---|---|---|---|---|---|
| Vinyals et al., 2015 | Sequence | Seq2Seq | Attention (AR) | Beam Search | Immitation (SL) |
| Bello et al., 2017 | Sequence | Seq2seq | Attention (AR) | Sampling | Actor-critic (RL) |
| Khalil et al., 2017 | Sparse Graph | Structure2vec | MLP (AR) | Greedy Search | DQN (RL) |
| Deudon et al., 2018 | Full Graph | Transformer Encoder | Attention (AR) | Sampling + Local Search | Actor-critic (RL) |
| Kool et al., 2019 | Full Graph | Transformer Encoder | Attention (AR) | Sampling | Rollout (RL) |
| Joshi et al., 2019 | Sparse Graph | Residual Gated GCN | MLP Heatmap (NAR) | Beam Search | Immitation (SL) |
| Ma et al., 2020 | Full Graph | GCN | RNN + Attention (AR) | Sampling | Rollout (RL) |
Recent Advances and Avenues for Future Work
With the unified 5-stage pipeline in place, let us highlight some recent advances and trends in deep learning for routing problems. We will also provide some future research directions with a focus on improving generalization to large-scale and real-world instances.
Leveraging Equivariance and Symmetries
One of the most influential early works, the autoregressive Attention Model [Kool et al., 2019], considers TSP as a Seq2Seq language translation problem and sequentially constructs TSP tours as permutations of cities. One immediate drawback of this formulation is that it does not consider the underlying symmetries of routing problems.
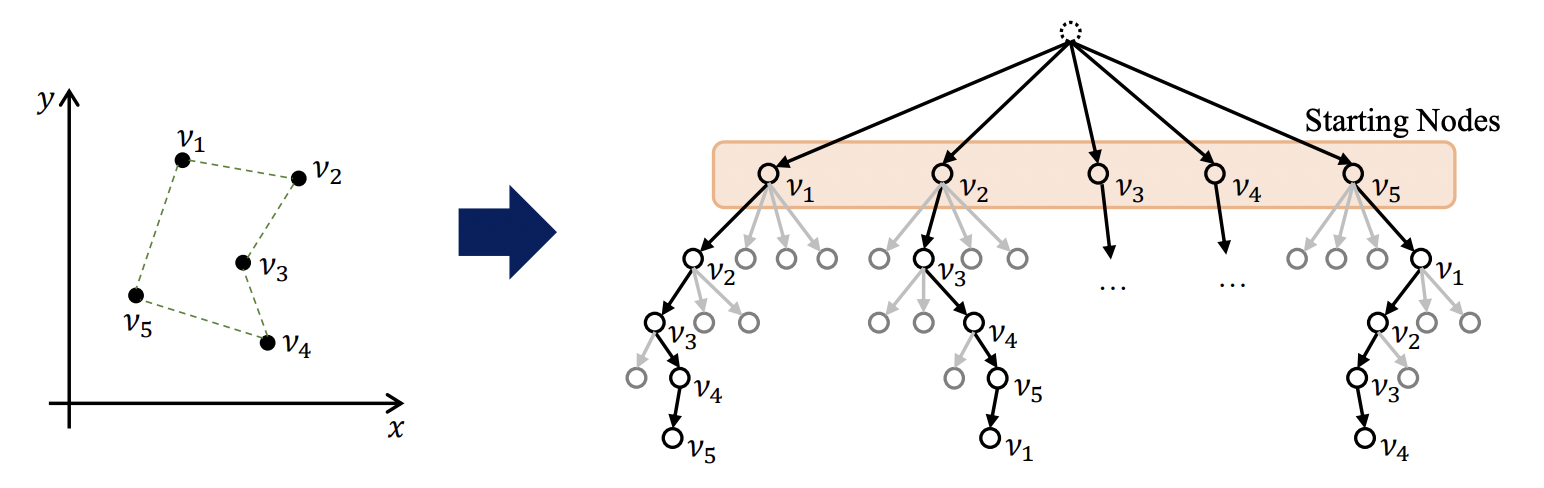
POMO: Policy Optimization with Multiple Optima [Kwon et al., 2020] proposes to leverage invariance to the starting city in the constructive autoregressive formulation. They train the same Attention Model, but with a new reinforcement learning algorithm (step 5 in the pipeline) which exploits the existence of multiple optimal tour permutations.

Similarly, a very recent ugrade of the Attention model by Ouyang et al., 2021 considers invariance with respect to rotations, reflections, and translations (i.e., the Euclidean symmetry group) of the input city coordinates. They propose an autoregressive approach while ensuring invariance by performing data augmentation during the problem definition stage (pipeline step 1) and using relative coordinates during graph encoding (pipeline step 2). Their approach shows particularly strong results on zero-shot generalization from random instances to the real-world TSPLib benchmark suite.
Future work may follow the Geometric Deep Learning (GDL) blueprint for architecture design. GDL tells us to explicitly think about and incorporate the symmetries and inductive biases that govern the data or problem at hand. As routing problems are embedded in euclidean coordinates and the routes are cyclical, incorporating these contraints directly into the model architectures or learning paradigms may be a principled approach to improving generalization to large-scale instances greater than those seen during training.
Improved Graph Search Algorithms
Another influential research direction has been the one-shot non-autoregressive Graph ConvNet approach [Joshi et al., 2019]. Several recent papers have proposed to retain the same Gated GCN encoder (pipeline step 2) while replacing the beam search component (pipeline step 4) with more powerful and flexible graph search algorithms, e.g., Dynamic Programming [Kool et al., 2021] or Monte-Carlo Tree Search (MCTS) [Fu et al., 2020].

The GCN + MCTS framework by Fu et al. in particular has a very interesting approach to training models efficiently on trivially small TSP and successfully transferring the learnt policy to larger graphs in a zero-shot fashion (something that the original GCN + Beam Search by Joshi et al. struggled with). They ensure that the predictions of the GCN encoder generalize from small to large TSP by updating the problem definition (pipeline step 1): large problem instances are represented as many smaller sub-graphs which are of the same size as the training graphs for the GCN, and then merge the GCN edge predictions before performing MCTS.
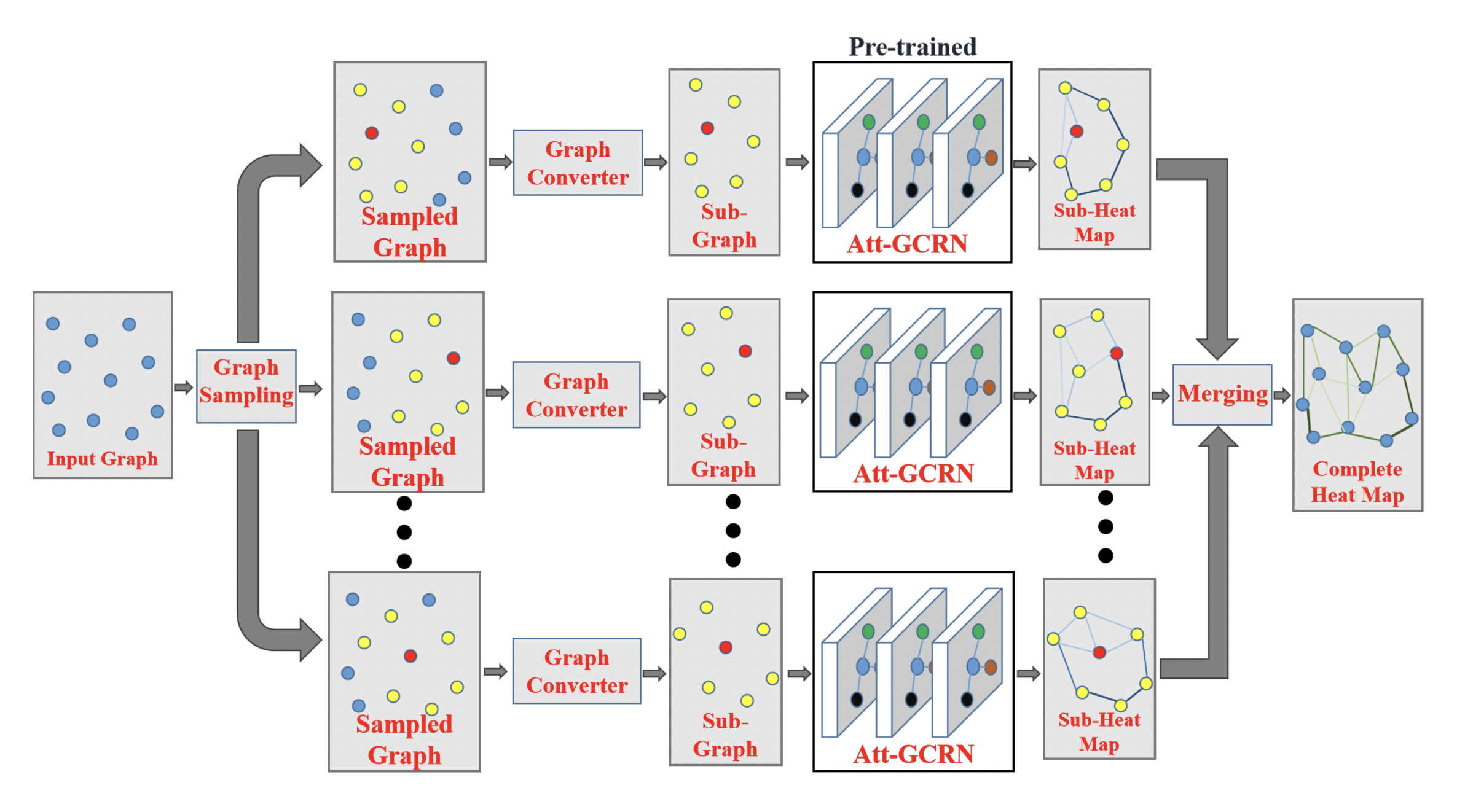
Originally proposed by Nowak et al., 2018, this divide-and-conquer strategy ensures that the embeddings and predictions made by GNNs generalize well from smaller to larger TSP instances up to 10,000 nodes. Fusing GNNs, divide-and-conquer, and search strategies has similarly shown promising results for tackling large-scale CVPRs up to 3000 nodes [Li et al., 2021].
Overall, this line of work suggests that stronger coupling between the design of both the neural and symbolic/search components of models is essential for out-of-distribution generalization [Lamb et al., 2020]. However, it is also worth noting that designing highly customized and parallelized implementations of graph search on GPUs may be challenging for each new problem.
Learning to Improve Sub-optimal Solutions
Recently, a number of papers have explored an alternative to constructive AR and NAR decoding schemes which involves learning to iteratively improve (sub-optimal) solutions or learning to perform local search, starting with Chen et al., 2019 and Wu et al., 2021. Other notable papers include the works of Cappart et al., 2021, da Costa et al., 2020, Ma et al., 2021, Xin et al., 2021, and Hudson et al., 2021.
In all these works, since deep learning is used to guide decisions within classical local search algorithms (which are designed to work regardless of problem scale), this approach implicitly leads to better zero-shot generalization to larger problem instances compared to the constructive approaches. This is a very desirable property for practical implementations, as it may be intractable to train on very large or real-world TSP instances.
Notably, NeuroLKH [Xin et al., 2021] uses edge probability heatmaps produced via GNNs to improve the classical Lin-Kernighan-Helsgaun algorithm and demonstrates strong zero-shot generalization to TSP with 5000 nodes as well as across TSPLib instances.
For the interested reader, DeepMind’s Neural Algorithmic Reasoning research program offers a unique meta-perspective on the intersection of neural networks with classical algorithms.
A limitation of this line of work is the prior need for hand-designed local search algorithms, which may be missing for novel or understudied problems. On the other hand, constructive approaches are arguably easier to adapt to new problems by enforcing constraints during the solution decoding and search procedure.
Learning Paradigms that Promote Generalization
Future work could look at novel learning paradigms (pipeline step 5) which explicitly focus on generalization beyond supervised and reinforcement learning, e.g., Hottung et al., 2020 explored autoencoder objectives to learn a continuous space of routing problem solutions.
At present, most papers propose to train models efficiently on trivially small and random TSPs, then transfer the learnt policy to larger graphs and real-world instances in a zero-shot fashion. The logical next step is to fine-tune the model on a small number of specifc problem instances. Hottung et al., 2021 take a first step towards this by proposing to finetune a subset of model paramters for each specific problem instance via active search. In future work, it may be interesting to explore fine-tuning as a meta-learning problem, wherein the goal is to train model parameters specifically for fast adaptation to new data distributions and problems.
Another interesting direction could explore tackling understudied routing problems with challenging constraints via multi-task pre-training on popular routing problems such as TSP and CVPR, followed by problem-specific finetuning. Similar to language modelling as a pre-training objective in Natural Language Processing, the goal of pre-training for routing would be to learn generally useful latent representations that can transfer well to novel routing problems.
Improved Evaluation Protocols
Beyond algorithmic innovations, there have been repeated calls from the community for more realistic evaluation protocols which can lead to advances on real-world routing problems and adoption by industry [Francois et al., 2019, Yehuda et al., 2020]. Most recently, Accorsi et al., 2021 have provided an authoritative set of guidelines for experiment design and comparisons to classical Operations Research (OR) techniques. They hope that fair and rigorous comparisons on standardized benchmarks will be the first step towards the integration of deep learning techniques into industrial routing solvers.
In general, it is encouraging to see recent papers move beyond showing minor performance boosts on trivially small random TSP instances, and towards embracing real-world benchmarks such as TSPLib and CVPRLib. Such routing problem collections contain graphs from cities and road networks around the globe along with their exact solutions, and have become the standard testbed for new solvers in the OR community.
At the same time, we must be vary to not ‘overfit’ on the top n TSPLib or CVPRLib instances that every other paper is using. Thus, better synthetic datasets go hand-in-hand for benchmarking progress fairly, e.g., Queiroga et al., 2021 recently proposed a new libarary of synthetic 10,000 CVPR testing instances. Additionally, one can assess the robustness of neural solvers to small perturbations of problem instances with adversarial attacks, as proposed by Geisler et al., 2021.
Regular competitions on freshly curated real-world datasets, such as the ML4CO competition at NeurIPS 2021 and AI4TSP at IJCAI 2021, are another great initiative to track progress in the intersection of deep learning and routing problems.
We highly recommend the engaging panel discussion and talks from ML4CO, NeurIPS 2021, available on YouTube.
Summary
This blogpost presents a neural combinatorial optimization pipeline that unifies recent papers on deep learning for routing problems into a single framework. Through the lens of our framework, we then analyze and dissect recent advances, and speculate on directions for future research.
The following table highlights in Red the major innovations and contributions for recent papers covered in the previous sections.
| Paper | Definition | Graph Embedding | Solution Decoding | Solution Search | Policy Learning |
|---|---|---|---|---|---|
| Kwon et al., 2020 | Full Graph | Transformer Encoder | Attention (AR) | Sampling | POMO Rollout (RL) |
| Fu et al., 2020 | Sparse Sub-graphs | Residual Gated GCN | MLP Heatmap (NAR) | MCTS | Immitation (SL) |
| Kool et al., 2021 | Sparse Graph | Residual Gated GCN | MLP Heatmap (NAR) | Dynamic Programming | Immitation (SL) |
| Ouyang et al., 2021 | Full Graph + Data Augmentation | Equivariant GNN | Attention (AR) | Sampling + Local Search | Policy Rollout (RL) |
| Wu et al., 2021 | Sequence + Position | Transformer Encoder | Transformer Decoder (L2I) | Local Search | Actor-critic (RL) |
| da Costa et al., 2020 | Sequence | GCN | RNN + Attention (L2I) | Local Search | Actor-critic (RL) |
| Ma et al., 2021 | Sequence + Cyclic Position | Dual Transformer Encoder | Dual Transformer Decoder (L2I) | Local Search | PPO + Curriculum (RL) |
| Xin et al., 2021 | Sparse Graph | GAT | MLP Heatmap (NAR) | LKH Algorithm | Immitation (SL) |
| Hudson et al., 2021 | Sparse Dual Graph | GAT | MLP Heatmap (NAR) | Guided Local Search | Immitation (SL) |
As a final note, we would like to say that the more profound motivation of neural combinatorial optimization may NOT be to outperform classical approaches on well-studied routing problems. Neural networks may be used as a general tool for tackling previously un-encountered NP-hard problems, especially those that are non-trivial to design heuristics for. We are excited about recent applications of neural combinatorial optimization for designing computer chips, optimizing communication networks, and genome reconstruction, and are looking forward to more in the future!
Acknowledgements: We would like to thank Goh Yong Liang, Yongdae Kwon, Yining Ma, Zhiguang Cao, Quentin Cappart, and Simon Geisler for helpful feedback and discussions.